Trees Data Structure

Hi everyone, inside this article we will see the concept about Trees Data Structure.

In data structure and algorithms, a tree is a nonlinear hierarchical data structure that is used to represent a set of elements, such as values or objects, and the relationships between them.

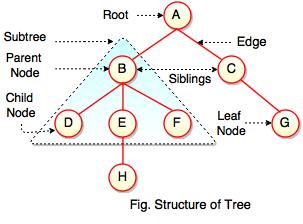
A tree consists of nodes and edges, where the nodes represent the elements, and the edges represent the relationships between them. The topmost node in the tree is called the root node, and the nodes that do not have any children are called leaves.

Trees are widely used in computer science and are used to solve a wide range of problems. Some of the common applications of trees include:

1. Storing hierarchical data, such as file systems, organization charts, and family trees.
2. Representing sorted data, such as binary search trees.
3. Implementing algorithms, such as AVL trees, red-black trees, and B-trees.
4. Encoding and compressing data, such as Huffman coding.

There are many types of trees in data structure and algorithms, including:

1. Binary tree: A tree where each node has at most two children.
2. AVL tree: A self-balancing binary search tree, where the heights of the left and right subtrees differ by at most one.
3. Red-black tree: A self-balancing binary search tree, where each node is colored either red or black, and the root is black.
4. B-tree: A self-balancing tree that is used to store large amounts of data on disk.
5. Trie: A tree-like data structure used to store strings, where each node represents a single character.
6. Heap: A tree-based data structure used to implement priority queues.
7. Decision tree: A tree used in machine learning to make decisions based on input data.

Each type of tree has its own set of characteristics and applications, and choosing the right type of tree for a specific problem is an important consideration when designing algorithms or data structures.

Important Terms of Trees Data Structure

Here are some important terms related to trees data structure:

1. Root: The root is the topmost node of the tree, and it has no parent.
2. Node: A node is a single element of the tree that contains a value and links to its child nodes.
3. Parent: A node that has one or more child nodes is called a parent node.
4. Child: A node that is directly below a parent node is called a child node.
5. Siblings: Nodes that share the same parent node are called siblings.
6. Leaf: A leaf node is a node that has no child nodes.
7. Depth: The depth of a node is the number of edges between the node and the root of the tree.
8. Height: The height of a tree is the maximum depth of any node in the tree.
9. Subtree: A subtree is a tree that is rooted at a node and contains all of its descendants.
10. Binary tree: A binary tree is a tree in which each node has at most two child nodes, called the left child and the right child.
11. Complete binary tree: A complete binary tree is a binary tree in which every level of the tree is fully filled, except possibly for the last level, which is filled from left to right.
12. Binary search tree: A binary search tree is a binary tree in which the values of the left child nodes are less than the value of the parent node, and the values of the right child nodes are greater than the value of the parent node.

Understanding these terms is essential for working with trees data structure and implementing algorithms that operate on them.

Basic Operations of Trees Data Structure

The basic operations of trees data structure include:

1. Insertion: This operation adds a new node to the tree.
2. Deletion: This operation removes a node from the tree.
3. Traversal: This operation visits all the nodes in the tree and performs some operation on each of them. There are several ways to traverse a tree, such as pre-order, in-order, and post-order traversal.
4. Searching: This operation searches the tree for a specific value.
5. Finding the minimum and maximum values: This operation finds the node with the minimum or maximum value in the tree.
6. Finding the height: This operation finds the height of the tree, which is the length of the longest path from the root to a leaf node.
7. Finding the depth: This operation finds the depth of a node, which is the length of the path from the root to the node.
8. Finding the size: This operation finds the number of nodes in the tree.
9. Checking if the tree is balanced: This operation checks if the tree is balanced, meaning that the heights of the left and right subtrees of every node differ by at most one.
10. Checking if the tree is a binary search tree: This operation checks if the tree is a binary search tree, meaning that the values of the left child nodes are less than the value of the parent node, and the values of the right child nodes are greater than the value of the parent node.

These basic operations are the building blocks for more complex algorithms that operate on trees, and they are essential for implementing many common tree algorithms.

Key points about Trees Data Structure

Here are some key points about trees data structure:

1. A tree is a hierarchical data structure consisting of nodes and edges.
2. A tree is defined by a root node, which has zero or more child nodes.
3. Each child node in a tree has a parent node, except for the root node which has no parent.
4. A node with no children is called a leaf node, and all other nodes are called internal nodes.
5. The level of a node in a tree is the number of edges from the root node to that node.
6. The height of a tree is the number of levels from the root node to the deepest leaf node.
7. A binary tree is a special type of tree where each node has at most two child nodes.
8. There are many different types of trees, including AVL trees, B-trees, red-black trees, and tries.
9. Trees can be used to represent hierarchical data, store sorted data, implement algorithms, and compress data.
10. Common operations on trees include inserting, deleting, and searching for nodes.
11. Tree traversal refers to the process of visiting all the nodes in a tree, typically in a specific order.
12. The performance of tree operations can be analyzed using the concepts of time and space complexity.

Overall, trees are a fundamental data structure in computer science, with a wide range of applications in many areas of computing. Understanding the characteristics and key points of trees is important for designing and implementing efficient algorithms and data structures.

We hope this article helped you to understand about Trees Data Structure in a very detailed way.

Online Web Tutor invites you to try Skillshike! Learn CakePHP, Laravel, CodeIgniter, Node Js, MySQL, Authentication, RESTful Web Services, etc into a depth level. Master the Coding Skills to Become an Expert in PHP Web Development. So, Search your favourite course and enroll now.

If you liked this article, then please subscribe to our YouTube Channel for PHP & it’s framework, WordPress, Node Js video tutorials. You can also find us on Twitter and Facebook.