Hi everyone, inside this article we will see the concept about Basics of Graph Algorithm.
Graph algorithms are a set of techniques used to traverse, search, manipulate, and analyze graphs or networks. A graph is a collection of nodes or vertices that are connected by edges or links.
Graph algorithms are used in a wide variety of applications, such as social networks, transportation networks, computer networks, and financial markets.
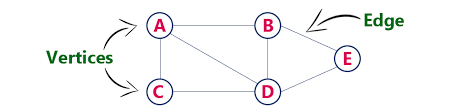
Components of a Graph
The components of a graph include:
- Vertices or Nodes: These are the basic elements of a graph. Vertices represent the objects or entities in the graph. In a social network, for example, vertices could represent people, while in a transportation network, vertices could represent cities.
- Edges or Links: These are the connections between vertices in a graph. Edges represent the relationships or interactions between objects or entities in the graph. In a social network, for example, edges could represent friendships or connections between people, while in a transportation network, edges could represent roads or routes between cities.
- Weight or Cost: This is an optional attribute that can be assigned to edges in a graph to represent the cost, distance, or other quantitative value associated with that edge. For example, in a transportation network, the weight of an edge could represent the distance between two cities.
- Directed or Undirected: A graph can be either directed or undirected. In an undirected graph, edges do not have a direction, meaning that they connect vertices in both directions. In a directed graph, edges have a direction, meaning that they connect vertices in a specific order.
- Connected or Disconnected: A graph can be either connected or disconnected. A connected graph is one in which there is a path between any two vertices in the graph. A disconnected graph is one in which there are one or more vertices that are not connected to any other vertices in the graph.
- Components: A graph can have one or more components. A component is a subset of vertices that are connected to each other by edges, but are not connected to any vertices outside of that subset. In a social network, for example, there could be multiple components representing different groups of people who are not connected to each other.
Overall, understanding the components of a graph is important for designing and implementing graph algorithms, as well as for analyzing and interpreting graph data.
Basic Properties of a Graph
The basic properties of a graph include:
- Order: The order of a graph is the number of vertices or nodes it contains.
- Size: The size of a graph is the number of edges or links it contains.
- Degree: The degree of a vertex is the number of edges that are incident to it. In a directed graph, there are two types of degree: in-degree, which is the number of edges pointing towards a vertex, and out-degree, which is the number of edges pointing away from a vertex.
- Path: A path is a sequence of vertices that are connected by edges in a graph. The length of a path is the number of edges it contains.
- Cycle: A cycle is a path that starts and ends at the same vertex.
- Connectedness: A graph is said to be connected if there is a path between any two vertices in the graph. Otherwise, it is disconnected.
- Components: A component is a subset of vertices that are connected to each other by edges, but are not connected to any vertices outside of that subset.
- Weighted edges: An edge can be weighted by assigning a numerical value or weight to it. The weight of an edge can represent distance, cost, or any other value associated with that edge.
- Directed or Undirected: A graph can be either directed or undirected. In an undirected graph, edges do not have a direction, meaning that they connect vertices in both directions. In a directed graph, edges have a direction, meaning that they connect vertices in a specific order.
Overall, these properties of a graph are important for understanding and analyzing the structure of a graph, and for designing and implementing graph algorithms.
Usage of Graph Algorithms
Graph algorithms have a wide range of applications across different fields.
Advantages of graphs:
- Efficient data representation: Graphs are a powerful data structure that can represent complex relationships and structures in a concise and efficient manner.
- Powerful visualization: Graphs can be visualized in many ways, including as network diagrams, charts, and graphs. These visualizations can help to reveal patterns, trends, and relationships in data.
- Easy to manipulate: Graphs can be easily manipulated and analyzed using algorithms, making them useful for a wide range of applications in fields such as computer science, operations research, and social sciences.
- Flexibility: Graphs can be used to model a wide variety of systems, from computer networks to social networks to transportation networks. They are not limited to any particular domain or field.
Disadvantages of graphs:
- Complex to construct: Building a graph can be time-consuming and complex, especially when the relationships and connections between vertices are not well-defined.
- Large memory requirements: Graphs can consume large amounts of memory, especially when they contain many vertices and edges.
- Difficult to analyze: Analyzing a graph can be challenging, especially when it contains many vertices and edges. There are many algorithms available for analyzing graphs, but choosing the right one for a particular problem can be difficult.
- Difficult to interpret: Graphs can be difficult to interpret when they contain many vertices and edges or when the relationships between vertices are complex. This can make it difficult to draw meaningful conclusions from the data.
Overall, graph algorithms are a powerful tool for analyzing and understanding complex relationships and networks in a wide variety of fields. They enable us to optimize systems, predict behavior, and make informed decisions based on data-driven insights.
Types of Graph Algorithms
There are many different types of graph algorithms, each with its own objectives and techniques. Here are some of the most common types:
- Traversal algorithms: These algorithms are used to visit all the nodes in a graph, usually in a specific order. Depth-first search and breadth-first search are examples of traversal algorithms.
- Shortest path algorithms: These algorithms are used to find the shortest path between two nodes in a graph. Dijkstra’s algorithm and Bellman-Ford algorithm are examples of shortest path algorithms.
- Minimum spanning tree algorithms: These algorithms are used to find the minimum spanning tree of a graph, which is a tree that connects all the nodes with the minimum total weight. Kruskal’s algorithm and Prim’s algorithm are examples of minimum spanning tree algorithms.
- Flow algorithms: These algorithms are used to find the maximum flow in a network, which is the maximum amount of flow that can be sent from a source node to a sink node through the network. Ford-Fulkerson algorithm and Edmonds-Karp algorithm are examples of flow algorithms.
- Clustering algorithms: These algorithms are used to group nodes in a graph into clusters or communities, which can be useful in social network analysis and other fields. Girvan-Newman algorithm and Louvain algorithm are examples of clustering algorithms.
- Centrality algorithms: These algorithms are used to identify the most important nodes in a graph, based on factors such as degree, betweenness, and eigenvector centrality. Betweenness centrality and eigenvector centrality are examples of centrality algorithms.
- Matching algorithms: These algorithms are used to find a maximum matching or minimum weight matching in a graph, which is a set of edges that do not overlap and cover as many nodes as possible. Hopcroft-Karp algorithm and Edmonds’ algorithm are examples of matching algorithms.
Overall, graph algorithms are a powerful tool for analyzing and understanding complex relationships and networks, and they have many practical applications in a wide variety of fields.
We hope this article helped you to understand Basics of Graph Algorithms in a very detailed way.
Online Web Tutor invites you to try Skillshike! Learn CakePHP, Laravel, CodeIgniter, Node Js, MySQL, Authentication, RESTful Web Services, etc into a depth level. Master the Coding Skills to Become an Expert in PHP Web Development. So, Search your favourite course and enroll now.
If you liked this article, then please subscribe to our YouTube Channel for PHP & it’s framework, WordPress, Node Js video tutorials. You can also find us on Twitter and Facebook.
